Throughput is an important performance indicator of Wireless Sensor Network (WSN). It directly reflects the efficiency of wireless sensor network operation. How to improve throughput has always been a hotspot in wireless sensor network research.
RJ Lavery first established the classic Adhoc network point-to-point link model in the reference, and clarified the mathematical definition of the point-to-point link model throughput. With the throughput as the optimization goal, the author optimizes the two parameters of symbol rate and packet length that affect throughput, and obtains the optimal symbol rate and packet length under different conditions. Subsequently, Taesang Yoo et al. proposed a mathematical framework in the reference, which uses the three parameters of symbol rate, packet length and modulation constellation volume as optimization variables to optimize the point-to-point link throughput in MQAM modulation mode. Subsequent references are based on the models and assumptions presented in the references, and similar studies and optimization analyses are performed on the throughput of the links. However, the throughput optimization of the reference is based on the Ad hoc network point-to-point link model established by reference, and the research on wireless sensor network throughput is relatively rare.
In view of the above problems, this paper will focus on how to maximize the point-to-point link throughput in WSN. In order to maximize the throughput, this paper adopts the cross-layer optimization mechanism, which not only considers the two physical layer (PHY) main parameters of symbol rate and modulation constellation volume, but also considers the packet length of the MAC layer, through the PHY and MAC layer parameters. Joint optimization ensures that the throughput of the link can be optimized at different communication distances.
1 system model and assumptionsTo simplify the analysis, this paper only considers the point-to-point link between two communication nodes in the WSN. A point-to-point communication link in a WSN typically consists of a single transmitter, receiver, and wireless communication channel. Assume that the total length of each data packet sent by the transmitter node is K+C=L bits, where K is the useful information data length and C is the Cyclical Redundancy Check CRC, which is used to detect each data packet. The error in the code is C=16 bits in the simulation analysis of this paper. The receiver node uses the CRC to verify the received data packet. It is assumed that the CRC only performs error detection without error correction coding, and the CRC has sufficient redundancy to detect all errors of each data packet. When the data packet received by the receiver does not contain an error, an ACK feedback frame is sent to the transmitter to inform that the data has been correctly received; otherwise, a NACK feedback frame is sent. When the transmitting node receives the NACK frame, it retransmits the data packet, otherwise it transmits the next new data packet. In real-time communication, ACK is still likely to generate errors, resulting in a decrease in system throughput. For the sake of simplicity, it is assumed here that the ACK/NACK feedback frame does not suffer from errors during transmission.
According to the reference, the throughput of a point-to-point link can be defined as the number of bits of useful information successfully received per second. For a point-to-point transmission link based on the above model and assumptions, the throughput is:
Where b is the number of bits per modulation symbol, Rs is the symbol rate, and f(b, rs, L) is the packet successful transmission rate (PSR), which is defined as the probability of correctly receiving a data frame. The PSR is given by:
Where Pr is the signal received power and N0 is the half-edge power spectral density of the noise in the AWGN channel.
At the same time, the received signal-to-noise ratio is defined as: SNR=Pr/(N0.B) (4)
Where B=1 MHz is the system bandwidth. Comparing equations (3) and (4), the relationship between the symbol signal to noise ratio rs and the received signal to noise ratio SNR can be obtained as follows:
2 throughput layering optimization2.1 Physical layer parameter optimization
2.1.1 Symbol Rate Optimization
In order to find the optimal symbol rate so that the throughput of the link reaches a maximum value, the partial derivative of Rs is obtained for equation (1) and the derivative is zero, that is, the following differential equation for rs can be obtained:

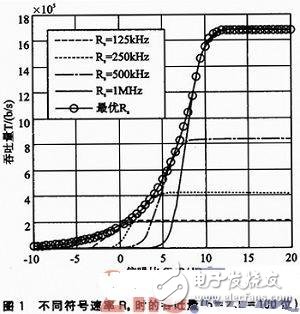
Figure 1 shows the throughput vs. SNR for four different symbol rate conditions. It can be seen that when the SNR is high, the link can support a higher symbol rate, thereby obtaining a larger throughput; however, when the SNR is lower than a certain value, the throughput is rapidly reduced, and a lower symbol should be adopted at this time. Rate to maintain a certain throughput. Therefore, in an actual communication system, in order to obtain an optimal throughput, adaptive rate adjustment must be performed according to SNR. According to formula (8), it can be solved when L=100 and b=2. When the SNR changes, the data rate Rs should be adjusted according to equation (9) to ensure that the optimal throughput is obtained. The optimal throughput curve obtained according to this is shown in Fig. 1.
2.1.2 Modulation constellation volume optimization