Machine learning algorithms can determine how to perform important tasks by generalizing examples. Such a goal is difficult to accomplish with manual programming, so machine learning is often feasible and cost-effective. As more data becomes available, more ambitious problems can be solved. Therefore, machine learning is widely used in fields such as computer sincerity. However, developing successful machine learning applications requires a lot of "black art" that is hard to find in textbooks.
1. Learning = Representation + Evaluation + Optimization
All machine learning algorithms generally consist of three components:
Representation: A classifier must be represented in some formal language that the computer can handle. Instead, choosing a representation for a learner is equivalent to choosing a set of classifiers that can be learned. This set is called the learner's hypothesis space. If a classifier is not in the hypothesis space, it cannot be learned. A related question is: how to represent the input, such as which features to use.
Evaluation: To distinguish between good classifiers and bad classifiers, an evaluation function is required. The evaluation function used inside the algorithm may be different from the evaluation function used outside the classifier, mainly for ease of optimization, and issues we will discuss in the next section.
Optimization: Finally, we need to find the one with the highest score among the language classifiers. The choice of optimization technique is the key to improving the efficiency of the learner, and also helps to determine whether the evaluation function of the classifier has multiple optimal values. It is common for beginners to start with off-the-shelf optimizers, but these are replaced by specially designed optimizers.
2. "Generalization ability" is critical, "test data" verification is critical!
The main goal of machine learning is to generalize to examples outside the training set. Because no matter how much data there is, it is unlikely to see the exact same example again in a test. It's easy to have good performance on the training set. The most common mistake made by beginners in machine learning is to test a model on training data, creating the illusion of success. If the chosen classifier is tested on new data, in general, the results are often close to random guessing. So, if you hire someone else to build a classifier, be sure to keep some data for yourself to test against the classifier they give you. Conversely, if someone hires you to build a classifier, keep a portion of the data for final testing of your classifier.
3. Data alone is not enough, the combination of knowledge works better!
Targeting generalization ability has another consequence: data alone is not enough, no matter how much data you have. Is this frustrating. So how can we expect it to learn something? However, the functions we want to learn in the real world are not all extracted from mathematically possible functions! In fact, using general assumptions - e.g. smoothness, similarity Samples with similar classifications, limited dependencies, or limited complexity - tend to do well enough, which is much of the reason why machine learning is so successful. Like deduction, induction (what the training model does) is a knowledge lever - it transforms a small amount of knowledge input into a large amount of knowledge output. Induction is a more powerful lever than deduction, requiring less knowledge to produce useful results. However, it still requires greater than zero knowledge input to work. As with any lever, the more you put in, the more you get.
In retrospect, the need for knowledge during training is not surprising. Machine learning is not magic. Like all engineering, programming is a lot of work: we have to build everything from scratch. The process of training is more like farming, where most of the work is done naturally. Farmers combine seeds with nutrients to grow crops. Training models combine knowledge with data to write programs.
4. "Overfitting" makes machine learning illusions!
A classifier (or a part of it) can create an "illusion" if the knowledge and data we have is insufficient to fully determine the correct classifier. The obtained classifier is not based on reality, but only encodes the randomness of the data. This problem, known as overfitting, is a thorny problem in machine learning. If your training model outputs a classifier that is 100% accurate on the training data but only 50% accurate on the test data, then in fact, the overall output accuracy of the classifier on both sets may be about approx. is 75%, it is overfitting.
In the field of machine learning, everyone knows about overfitting. But overfitting comes in many forms that people often don't realize right away. One way to understand overfitting is to decompose the generalization error into bias and variance. Bias is the tendency of a model to keep learning the same mistakes. Variance refers to the tendency of the model to learn random signals regardless of the true signal. Linear models have high bias because the model cannot make adjustments when the boundary between two classes is not a hyperplane. Decision trees do not have this problem because they can represent any Boolean function. But on the other hand, decision trees can have a lot of variance: if trained on different training sets, the resulting decision trees are usually very different, when in fact they should be the same.
Cross-validation can help combat overfitting, for example, by using cross-validation to select the optimal size of a decision tree for training. But this is not a panacea, because if we generate too many parameter choices with cross-validation, it will start to overfit itself.
Besides cross-validation, there are many ways to deal with overfitting. The most popular is to add a regularization term to the evaluation function. For example, this can penalize classifiers with more terms, which can help generate classifiers with simpler parameter structures and reduce the space for overfitting. Another approach is to perform a statistical significance test like a chi-square test before adding the new structure to determine whether the distribution of the classes really differs before and after adding the new structure. These techniques are especially useful when there is very little data. Nonetheless, you should be skeptical of claims that some method solves the overfitting problem perfectly. Reducing overfitting (variance) makes it easy for a classifier to fall into its opposite underfitting error (bias). If you want to avoid both cases, you need to train a perfect classifier. Without prior information, no one method is always the best (there is no such thing as a free lunch).
5. The biggest problem in machine learning is the "curse of dimensionality"!
Besides overfitting, the biggest problem in machine learning is the curse of dimensionality. The term was coined by Bellman in 1961 to refer to the fact that many algorithms that work well in low dimensions will not work well when the input dimension is high. But in machine learning, it has a wider meaning. As the sample dimension (number of features) increases, it becomes increasingly difficult to generalize correctly because the fixed-size training set gradually shrinks the coverage of the input space.
The general problem with higher dimensions is that human intuitions from the 3D world often do not apply to higher dimensional spaces. In high dimensions, most of the data for a multivariate Gaussian distribution is not close to the mean, but in a "shell" that is farther and farther around it; moreover, most of the volume of a high-dimensional distribution is distributed on the surface, not the body. If a constant number of samples are uniformly distributed in a high-dimensional hypercube, then beyond a certain number of dimensions, most samples will be closer to a face of the hypercube than to their nearest neighbors. Furthermore, if we approximate a hypersphere by embedding the hypercube, then in high dimensions almost all of the volume of the hypercube is outside the hypersphere. This is bad news for machine learning, as one type of shape can often be approximated by another, but fails in high-dimensional spaces.
Building a 2D or 3D classifier is easy; we can find reasonable boundaries between samples of different classes just by visual inspection. But in high dimensions, it is difficult for us to understand the distribution structure of the data. This in turn makes it difficult to design a good classifier. In short, one might think that collecting more features must not have a negative effect, since at best they just don't provide new information about the classification. But in fact, the effects of the curse of dimensionality may outweigh the benefits of adding features.
6. The relationship between "theoretical guarantee" and "practical discrepancy"
Machine learning papers are full of theoretical guarantees. The most common guarantee is about the constraint on the number of training samples that preserves the model's good generalization ability. First, the problem is clearly provable. Induction is often the opposite of deduction: with deduction, you can be sure that the conclusion is correct; in induction, all assumptions are discarded. Perhaps this is the ancient wisdom handed down. The major breakthrough of the last decade has been the recognition of the fact that the results of induction are provable, especially when we are willing to give probabilistic guarantees.
What such constraints mean must be considered. This does not mean that if your network returns a hypothesis that is consistent with a particular training set, then that hypothesis is likely to generalize well. Rather, given a sufficiently large training set, your network is likely to return a hypothesis that generalizes well or fails to yield a consistent hypothesis. Such constraints also do not teach us how to choose a good hypothesis space. It just tells us that if the hypothesis space contains good classifiers, the probability of the network training a weak classifier decreases as the training set grows. If the hypothesis space is reduced, the constraints will increase, but the probability of training a strong classifier will also decrease.
Another common theoretical guarantee is asymptotic: if the input data size is infinite, then the network must output a strong classifier. Sounds plausible, but because of the asymptotic nature, choosing one network over another would be rash. In practice, we are rarely in asymptotics. From the bias-variance trade-off discussed above, if network A is better than network B with a lot of data, then B tends to be better than A with limited data.
Theoretical assurance exists in machine learning not only as a criterion for judging actual decisions, but also as a method of understanding and a driving force for designing algorithms. For this, it is very useful. In fact, over the years, it is the combination of theory and practice that has led to the leap forward in machine learning. Note: Learning is a complex phenomenon, it makes sense in theory and works in practice, and it does not mean that the former is the cause of the latter.
7. “Feature engineering†is the key to machine learning
In the end, some machine learning projects are wildly successful and some fail. What causes this? The most important factor is the feature used. The learning process is easy if you get a lot of independent and class-related features. Conversely, if a class is an extremely complex function of a feature, your model may fail to learn that function. In general, the raw data format is not suitable for learning, but features can be built from it. This is the most important part of a machine learning project, and often the most interesting part, where intuition, creativity, "magic" and technology are just as important.
Beginners are often surprised how little time machine learning projects actually spend on machine learning. But it's not surprising when you factor in the time spent on chores like collecting, integrating, cleaning, and preprocessing data, and resolving errors in reconstructing data into features. Moreover, machine learning is not just about building a dataset and running a model once, it is usually an iterative process of running the model, analyzing the results, and modifying the dataset/model. Learning is the fastest part of it, but it depends on how proficient we are at it! Feature engineering is hard to do because it is domain specific, while model architectures are more applicable. However, there is no clear line between the two, which usually explains the better performance of those models that incorporate domain knowledge.
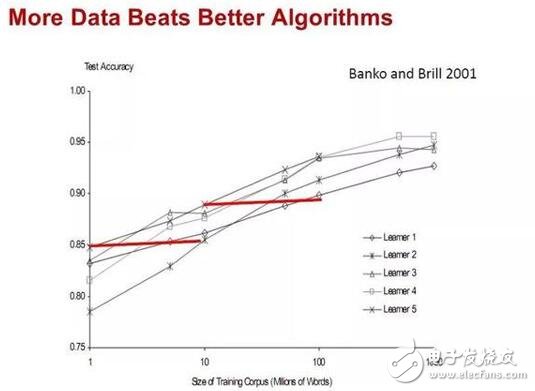
8. Remember: the amount of data is more important than the algorithm!
In most areas of computer science, time and memory are two scarce resources. But in machine learning, datasets are the third scarce resource. Over time, the bottleneck battle is constantly changing. In the 1980s, data was often the bottleneck. Now time is more precious. We have a huge amount of data available today, but not enough time to process it, so the data is sitting on hold. This creates a paradox: even though in principle a large amount of data means that more complex classifiers can be learned, in practice we tend to use simpler classifiers because complex classifiers mean more complex classifiers. long training time. Part of the solution is to come up with methods that can quickly learn complex classifiers, and there is indeed significant progress in this direction today.
Part of the reason why using a smarter algorithm is not as rewarding as expected is that it is no different than any other algorithm when first approximated. It will surprise you when you think that the difference between representations is similar to the difference between rules and neural networks. But the truth is that propositional rules can be easily encoded into neural networks, and there are similar relationships between other representations. The models are essentially all implemented by classifying nearby samples into the same category, the key difference being the meaning of "nearest neighbor". For non-uniformly distributed data, the model can produce widely different boundaries while producing the same predictions in important regions (regions with a large number of training examples, and thus where most text examples are likely to occur). This also explains why robust models can be unstable and still be accurate.
In general, we first consider the simplest models (eg, Naive Bayes instead of logisTIc regression, K-Nearest Neighbors instead of SVMs). The more complex the models are, the more attractive they are, but they are often difficult to use because you need to tweak a lot of nodes to get good results, and at the same time, their internals are extremely opaque.
Models can be divided into two main types: models with fixed size, such as linear classifiers, and models whose representational power increases with the dataset, such as decision trees. Fixed-scale models can only utilize limited data. A scalable model can theoretically fit any function, as long as there is a sufficiently large dataset, but the reality is very skinny, and there are always algorithmic limitations or computational costs. Also, existing datasets may not be enough due to the curse of dimensionality. For these reasons, smarter algorithms—those that make good use of data and computing resources—will end up with good results if you're willing to put in the effort to debug them. There is no very clear line between designing a model and learning a classifier; however, any given point of knowledge can be encoded into a model or learned from data. Therefore, model design is often an important part of machine learning projects, and designers preferably have relevant professional backgrounds.
9. "Single model" is difficult to achieve optimal, "multi-model integration" is the way out!
In the early days of machine learning development, everyone had a favorite model, with some a priori reasons for its superiority. Researchers develop a large number of variants of the model and select an optimal model from them. Subsequently, empirical comparisons of systems have shown that the best model varies with application, and systems containing many different models are starting to emerge. The current research begins by trying to debug different variants of multiple models and pick the one that performs best. But researchers are starting to notice that instead of selecting the best variant found, combining multiple variants yields better results (often a lot better) without increasing the effort.
Model ensembles are now the standard approach. The simplest of these techniques is the bagging algorithm, where we generate random variants of the training dataset simply by resampling, learn separate classifiers based on these variants, and integrate the results of these classifiers by voting. The feasibility of this method is that it greatly reduces the variance and only slightly increases the bias. In the boostTIng algorithm, the training examples have weights, and these weights are different, so each new classifier focuses on examples where the previous model would have made mistakes. In the stacking algorithm, the output of each individual classifier is used as input to "higher-level" models that combine these models in an optimal way.
There are many other methods, too many to list, but the general trend is ensemble learning on a larger and larger scale. Inspired by Netflix's bounty, teams around the world work to build the best video recommendation system. As the competition progresses, the competition team finds that the best results can be obtained by combining models from other teams, which also promotes team consolidation. Both the champion and runner-up models are ensemble models consisting of more than 100 small models, and the two ensemble models are combined to further improve the performance. Undoubtedly, larger ensemble models will emerge in the future.
10. "Simple" does not mean "accurate"!
Occam's razor principle states that entities should not be multiplied unless necessary. In machine learning, this usually means that, given two classifiers with the same training error, the simpler of the two is likely to have the lowest evaluation error. Evidence for this claim is ubiquitous in the literature, but there are actually plenty of counterexamples to disprove it, and the "no free lunch" theorem calls into question its veracity.

We also saw a counter-example earlier: ensemble models. Even if the training error has reached zero, the generalization error of the augmented ensemble model can continue to decrease by adding classifiers. Thus, counterintuitively, the number of parameters of a model is not necessarily related to its tendency to overfit.
A neat idea is to equate model complexity with the size of the hypothesis space, since a smaller space allows to characterize hypotheses with shorter codes. Similar bounds in the theoretical guarantees section might be interpreted as shorter hypothetical codes that generalize better. We can refine this further by encoding hypotheses shorter in a space with prior preferences. But seeing this as a demonstration of the trade-off between accuracy and simplicity is a circular argument: we make our preferred hypotheses simpler by design, and if they are accurate, it is because the preferred hypothesis is correct, not because in a particular Characterizes the "simplicity" of the underlying assumption.
11. "Representable" does not mean "learnable"!
All model representations applied to non-fixed scales actually have related theorems like "any function can be represented or infinitely approximated using this representation". This makes the preference of a certain representation method often ignore other elements. However, representation alone does not mean that the model can learn. For example, a decision tree model with more leaf nodes than training samples will not learn. In continuous spaces, it is common to use a fixed set of primitives to represent very simple functions that require infinite components.
Furthermore, if the evaluation function has many local optima in the hypothesis space (which is common), the model may not find an optimal function, even if it is representable. Given limited data, time, and storage space, standard models can only learn a small subset of the set of all possible functions, and this subset varies with the chosen representation method. Therefore, the key question is not "is the model representable", but "is the model learnable" and it is important to try different models (even ensemble models).
12. "Correlation" doesn't mean "causation"!
The point that correlation does not imply causation is brought up so often that it doesn't deserve criticism. However, some of the models we discuss may only learn correlations, but their results are often seen as representing causality. Is there a problem? If so, why do people still do it?
Often not, predictive models learn with the goal of using them as guides for action. When you find that people also buy diapers when they buy beer, placing beer next to a diaper may increase sales. But it is difficult to verify without actually conducting experiments. Machine learning is often used to deal with observational data, where predictors are not controlled by the model, as opposed to experimental data (controllable). Some learning algorithms may be able to mine potential causal relationships from observational data, but their utility is poor. Correlation, on the other hand, is just an indication of an underlying causal relationship that we can use to guide further research.
Galanz Microwave Oven Panel Membrane Switch
Microwave steam can be used in all kinds of food, the microwave oven before use the switch is the rotary switch, no food set, only by rotating for temperature adjustment, some people think that is very convenient, but the time is progressive, meet now microwave Membrane Switch, you will know a rotary switch is already obsolete. There are different patterns and different temperatures set on the membrane switch. The pattern is usually the pattern of food, so the pattern can be selected according to the different steamed food, and each pattern is also involved in the temperature, so as long as the pattern is selected, the temperature can be directly regulated systematically. Automated products bring more convenience to people, and the temperature and time can be displayed autonomously on the membrane switch.
Galanz Microwave Oven Panel Membrane Switch,Balances Membrane Switch,Analytical Balances Membrane Switch,Gloss Surface Membrane Keypad
Dongguan Nanhuang Industry Co., Ltd , https://www.soushine-nanhuang.com